Machine learning of fluid flows

Machine learning of fluid flows using the proper orthogonal decomposition (POD) and the dynamic mode decomposition (DMD) methods

1. Introduction

1.1 Background and Motivation

Fluid dynamics has long been challenging due to its inherent high-dimensionality and nonlinear behaviour. Traditional numerical approaches, while effective, often become computationally prohibitive when applied to complex flows, such as turbulent flows past a cylinder. In recent years, data-driven methods have emerged as promising alternatives by extracting the essential dynamics directly from high-fidelity simulation or experimental data. Two techniques, particularly Proper Orthogonal Decomposition (POD) and Dynamic Mode Decomposition (DMD), have gained prominence for their ability to identify coherent structures and predict temporal evolution in fluid flows.

POD, closely related to the singular value decomposition (SVD), decomposes complex flow fields into a set of orthogonal modes ordered by energy content. This enables a reduced-order representation of the flow, capturing the dominant features with a minimal number of modes. On the other hand, DMD builds upon this framework to extract dynamic information from the data, yielding modes associated with specific growth rates and frequencies. These methods facilitate efficient data compression and provide insights into the underlying physics, making them valuable for applications ranging from turbulence modelling to predictive control.

The motivation behind this project lies in harnessing these data-driven techniques to analyze and predict fluid flows. By focusing on a canonical problem of two-dimensional flow past a cylinder at a Reynolds number of 200, we aim to bridge the gap between theoretical developments in machine learning and practical applications in fluid dynamics. This approach reduces the complexity of high-dimensional datasets and paves the way for improved understanding and control of liquid systems.

1.2 Project Objectives

The primary objectives of this project are as follows:

1.2.1 Extraction of Coherent Structures

Develop a comprehensive understanding of the POD method by applying it to the sequential vorticity data of a 2D cylinder flow. This includes demonstrating how the energy content is distributed among the modes and determining the convergence behaviour as the number of time snapshots increases.

1.2.2 Dynamic Mode Analysis

Implement the DMD algorithm to identify dynamic modes and their associated eigenvalues. The project will examine whether DMD modes converge like the POD modes and assess their capability to capture the temporal evolution of the flow.

1.2.3 Prediction and Validation

Utilize the computed DMD modes and eigenvalues to predict future flow states. The accuracy of these predictions will be statistically validated using measures such as Pearson's correlation coefficient and probability distribution analysis, ensuring that the prediction aligns well with the observed data.

1.2.4 Integration and Reporting

Combine the insights from POD and DMD analyses into this research report and critically discuss the implications of these methods in the broader context of data-driven fluid dynamics.

2. Methodology

2.1 Data Acquisition and Preprocessing

The analysis begins with acquiring a high-dimensional dataset representing the vorticity field of a two-dimensional flow past a cylinder at a Reynolds number Re = 200. The dataset, which consists of M = 1052 time snapshots, is organized as a matrix   where each column is a vectorized snapshot of the flow, and n = 768 x 192 = 147456 corresponds to the number of spatial grid points.

The data is initially downloaded and stored in an HDF5 format file named "U_data.h5" using "load_xcyl2d_v2.ipynb". After loading the data, it is preprocessed to ensure the matrix is normalized correctly and centred (if necessary). This preprocessing is crucial for applying singular value decomposition (SVD) and dynamic mode decomposition (DMD).

2.2 Proper Orthogonal Decomposition (POD)

Proper Orthogonal Decomposition (POD) is a technique that identifies an optimal set of orthogonal basis functions (modes) that capture most of the system's energy. This is typically achieved via the singular value decomposition (SVD) of the data matrix U:

Where:

•   contains the left singular vectors (POD modes),
•  is a diagonal matrix with non-negative singular values  , and
•  contains the right singular vectors.

The singular values   measure the energy associated with each POD mode. In practice, we often truncate the decomposition to retain only the r most energetic modes, where r << n: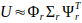

,

with  ,  , and  .

A convergence criterion is then established by studying the decay of the singular values. For instance, if the cumulative energy captured by the first m snapshots meets a predetermined threshold (e.g., 99% of the total energy), these m snapshots are deemed sufficient for constructing a robust reduced-order model.

2.3 Dynamic Mode Decomposition (DMD)

Dynamic Mode Decomposition (DMD) builds upon the POD framework to incorporate the temporal evolution of the system. DMD decomposes the data into modes associated with fixed oscillation frequencies and growth/decay rates. The algorithm proceeds as follows:

2.3.1 Data Splitting

The snapshot matrix U is split into two matrices:

U₁ = [u₁,u₂,...,u_M-1] and U₂ = [u₂,u₃,...,u_M]

where u_k denotes the k-th snapshot.

2.3.2 Low-Dimensional Projection

Using the POD modes Φ obtained from U₁, project the data onto the reduced space:

2.3.3 Approximation of the Linear Mapping

We assume that there exists a linear mapping A such that:

U₂ ≈ AU₁.

Projecting this relationship into the reduced space gives:

,

where    and   denotes the pseudo-inverse of  .

2.3.4 Eigen Decomposition

The eigenvalues and eigenvectors of  are computed:

,

The DMD modes in the original high-dimensional space are then given by:

.

2.3.5 Reconstruction and Dynamics

The temporal dynamics associated with each mode are expressed as:

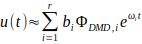
where  are the continuous-time eigenvalues and b_i are coefficients determined by projecting the initial condition onto the DMD modes.

2.4 Prediction and Validation

Once the DMD modes and eigenvalues are computed, they can be used to predict the future states of the flow. The prediction at a future time t is given by:

,

where b is determined from the initial condition u₀ via a least squares solution:

.

To assess the accuracy of the predictions, statistical validation methods are employed. For example, the Pearson's correlation coefficient r can be used to measure the linear correlation between the predicted and actual data:

,

where  and  represent the actual and predicted data points, respectively, and  and  are their corresponding means.

Additionally, we can analyze the probability distribution of the prediction errors to validate the model's performance further. Comparing these statistical measures between the training and testing datasets ensures the prediction model is robust and generalizes well beyond the training samples.

3. Results

3.1 Visualization of Modes

The first results focus on visualizing the dominant flow structures extracted from the data using Proper Orthogonal Decomposition (POD) and Dynamic Mode Decomposition (DMD).

3.1.1 POD Modes

Using the singular value decomposition (SVD) on the centred data matrix, the POD analysis revealed that the singular values decay rapidly, indicating that only a few modes are necessary to capture the majority of the energy in the system. The top three POD modes were extracted and reshaped to match the original spatial grid (768 x 192). These modes exhibit apparent spatial coherence, demonstrating that the dominant energy-containing structures in the flow are well-represented by these modes. The visualizations (colour-coded using a jet colour-map) reveal patterns corresponding to the most significant flow features.

Figure 1 illustrates the first three POD modes computed from the vorticity field of the cylinder flow at Re = 200. These modes capture the most energetic coherent structures, with the first 10 modes resolving 99% of the total energy. The spatial orthogonality and vortical patterns validate POD's ability to decompose the flow into a low-dimensional feature space, essential for reduced-order modelling.

The convergence of POD modes concerning the number of training snapshots m was analyzed to determine the minimum dataset size required to capture 99% of the system's energy. Figure 2 illustrates the cumulative energy captured by the first 10 POD modes as m increases. The analysis revealed that only 50 snapshots can achieve the 99% energy threshold, indicating rapid convergence of the POD modes. This result demonstrates that the dominant flow structures are well-represented even with a small subset of the data, highlighting the efficiency of POD in reducing high-dimensional fluid flow datasets. Beyond m = 50, additional snapshots contribute minimally to the energy captured by the leading modes, confirming that the training dataset size does not need to exceed this threshold for robust dimensionality reduction.

Figure 2 illustrates decay of singular values with increasing mode index, establishing the rapid drop in energy contribution from higher-order modes and cumulative energy captured by the first r modes, demonstrating that a small subset of modes captures the majority of the system's energy.

3.1.2 DMD Modes

Dynamic Mode Decomposition was applied to capture the temporal evolution of the flow. The DMD algorithm computed eigenvalues and eigenvectors of a low-dimensional linear operator approximating the system dynamics. The resulting DMD modes, also reshaped to the original spatial dimensions, show similar spatial coherence as the POD modes but with additional dynamic characteristics (oscillation frequencies and growth/decay rates). These modes provide insights into how the flow evolves and how different flow features contribute to the temporal dynamics.

Figure 3 illustrates the first three DMD modes extracted from the vorticity field of the cylinder flow at Re = 200. These modes capture spatio-temporal coherent structures, with eigenvalues reflecting oscillatory dynamics and stability. The spatial amplitude variations (colour-coded) and temporal evolution highlight DMD's ability to resolve dynamic features critical for predicting flow evolution. Unlike POD, DMD modes incorporate both spatial coherence and temporal growth/decay rates, essential for reduced-order modelling of transient phenomena.

The convergence of DMD eigenvalues concerning the number of training snapshots m was analyzed to determine the stability of the dominant dynamic mode. Figure 4 illustrates the real and imaginary components of the dominant DMD eigenvalue as m increases. The eigenvalue stabilizes significantly for m ≥ 400, indicating that approximately 400 snapshots are required to resolve the dominant oscillatory dynamics of the flow. This slower convergence compared to POD arises from DMD's emphasis on temporal coherence, which demands a richer dataset to capture transient or periodic features accurately. Beyond m = 400, the eigenvalue components remain nearly constant, confirming that the DMD operator converges with sufficient training data.

Figure 4 illustrates the convergence of dominant DMD eigenvalues with increasing snapshots.

3.2 Prediction Performance

The second part of the results evaluates the predictive capability of the DMD model using following statistical tools:

3.2.1 Pearson's Correlation Coefficient

The Pearson correlation coefficient between the actual and predicted snapshots was computed for several time instances. High correlation values (close to 1) indicate a strong linear relationship between the predicted and actual data. A time evolution plot of the correlation coefficient demonstrates that the predictions remain robust over the prediction horizon.

Figure 5 illustrates a comparison of an actual snapshot and its corresponding DMD prediction, highlighting the spatial agreement between the two.

Figure 6 illustrates the evolution of the Pearson's correlation coefficient over time, which confirms that the predictions closely follow the actual data.

3.2.2 Probability Distribution of Prediction Errors

In addition to Pearson's correlation, the prediction error was defined as the difference between the actual and predicted snapshots. A histogram (or probability distribution plot) of these errors was generated to examine their statistical properties. The resulting distribution helps to determine if the errors are normally distributed and whether there are significant outliers. A narrow, approximately Gaussian distribution of errors suggests that the DMD model is accurately capturing the dynamics of the flow.

Figure 7 illustrates a histogram of the prediction errors, demonstrating that the error distribution is centred near zero with limited spread, further validating the model's performance.

4. Discussion

4.1 Analysis of Findings

The two-dimensional cylinder flow data analysis through POD and DMD provided valuable insights into the underlying fluid dynamics. The following key findings were observed:

4.1.1 POD Analysis

The singular value decomposition (SVD) revealed a rapid decay in singular values, indicating that a limited number of modes capture most of the system's energy. When reshaped to the original spatial grid, the top POD modes displayed coherent spatial structures that clearly represent the dominant flow features. This result confirms the efficiency of POD in reducing high-dimensional data while retaining essential information.

4.1.2 DMD Analysis

The DMD algorithm extracted modes that incorporate both spatial and temporal dynamics. The DMD modes resembled the POD modes in spatial structure but provided additional dynamic information through the associated eigenvalues. The computed continuous-time eigenvalues, obtained by converting the discrete eigenvalues via the relation

offer insights into the growth, decay, and oscillatory behaviour of the flow structures.

4.1.3 Prediction Performance

The DMD model could reconstruct the flow field with high accuracy over time. The predictions were validated using two statistical measures:

4.1.3.1 Pearson's Correlation Coefficient

High correlation values between actual and predicted snapshots confirm that the model captures the linear relationship effectively.

4.1.3.2 Probability Distribution of Prediction Errors

A smooth probability density function of the prediction errors indicates that the errors are approximately Gaussian, with a narrow spread around zero. This behaviour suggests that the model's prediction errors are random and well-behaved.

Overall, the analysis demonstrates that combining POD and DMD provides a robust framework for extracting dominant features and predicting the evolution of fluid flow dynamics. The convergence of the modes and the high statistical agreement between predictions and actual data affirm the validity of the data-driven approach applied in this study.

4.2 Implication and Future Work

The findings of this project have several important implications and open up avenues for future research:

4.2.1 Implications for Fluid Dynamics Analysis

The successful application of POD and DMD to a complex fluid flow problem underscores the power of data-driven methods in fluid dynamics. These techniques enable efficient dimensionality reduction and provide physical insights into coherent structures and dynamic behaviour, which is essential for understanding turbulent flows. This approach can be particularly valuable when traditional numerical methods are computationally expensive.

4.2.2 Integration with Machine Learning

Although this study focused on linear techniques, integrating conventional machine learning algorithms (e.g., clustering, regression, or neural networks) could further enhance the predictive capabilities. Machine learning models could be used to optimize the selection of modes or refine the dynamic predictions by capturing non-linearities not fully addressed by linear model decomposition.

4.2.3 Enhanced Prediction Models

Future work could explore hybrid models that combine DMD with advanced machine learning techniques, such as deep learning-based auto-encoders, to capture more complex, non-linear dynamics. Moreover, investigating adaptive or time-varying modes could lead to more robust prediction models in the presence of external perturbations or changing flow conditions.

4.2.4 Applications Beyond Fluid Dynamics

The methodologies presented in this project are not limited to fluid dynamics. The model decomposition and dynamic prediction framework can be applied to other fields involving high-dimensional time-series data, such as climate modelling, financial forecasting, and biomedical signal processing. Future studies could explore cross-disciplinary applications, demonstrating the versatility and generalization of these data-driven techniques.

4.2.5 Computational Efficiency and Scalability

With ever-increasing data sizes in high-fidelity simulations and experiments, future research should also address the scalability of these methods. Exploring more efficient algorithms for SVD and eigen-decomposition, as well as leveraging parallel computing and GPU acceleration, could significantly enhance the practical applicability of POD and DMD in real-time monitoring and control of complex systems.

In summary, the current study validates the effectiveness of POD and DMD in analyzing and predicting fluid flows while highlighting several promising directions for future work. Incorporating advanced machine learning techniques and focusing on computational efficiency are compelling areas for further research.

5. Conclusion

5.1 Summary of Work

This project explored data-driven methods for analyzing and predicting fluid flow dynamics, focusing on a two-dimensional flow past a cylinder at Re = 200. The work began with the acquisition and pre-processing of high-dimensional vorticity data, structured as a matrix , where each column represents a time snapshot of the flow field.

Proper Orthogonal Decomposition (POD) was used and the data was decomposed into a set of orthogonal modes via singular value decomposition (SVD). The rapid decay in the singular values confirmed that only a few modes are required to capture the dominant energy of the system. These POD modes, when reshaped to match the original spatial grid, revealed coherent structures that encapsulate the essential features of the flow.

Dynamic Mode Decomposition (DMD) was then applied to incorporate temporal dynamics into the analysis. The DMD algorithm computed dynamic modes and their associated eigenvalues by splitting the dataset into time-shifted matrices and projecting them onto a reduced-order subspace. These eigenvalues were converted to continuous-time dynamics using the relation:

,

allowing for a reconstruction of the flow evolution. The DMD-based predictions were validated statistically using Pearson’s correlation coefficient and a smooth probability distribution of the prediction errors, which closely approximated a Gaussian profile centred around zero.

5.2 Final Remarks

The parallel use of POD and DMD in this project has demonstrated the potential of data-driven approaches to effectively reduce the complexity of high-dimensional fluid dynamics problems while capturing the essential features and dynamics. The high correlation between predicted and actual snapshots and the well-behaved error distribution confirm the robustness and accuracy of the DMD-based predictive model.

While the current implementation employs linear algebra techniques for model decomposition, future work could further integrate machine learning methodologies to enhance model performance and capture non-linear dynamics. Moreover, the scalable nature of these methods suggests promising applications in fluid dynamics and other fields dealing with high-dimensional time-series data.

In conclusion, this study provides a solid foundation for applying POD and DMD in data-driven fluid dynamics analysis. It paves the way for further advancements in predictive modelling and real-time flow control.

6. References

1. Holmes, P., Lumley, J. L., & Berkooz, G. (1996). Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.
2. Schmid, P. J. (2010). "Dynamic Mode Decomposition of Numerical and Experimental Data." Journal of Fluid Mechanics, 656, 5–28.
3. Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L., & Kutz, J. N. (2014). "On Dynamic Mode Decomposition: Theory and Applications." Journal of Computational Dynamics, 1(2), 391–421.
4. Kutz, J. N., Brunton, S. L., Brunton, B. W., & Proctor, J. L. (2016). Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems. SIAM.